What is the pattern of 4 9 14 19 24
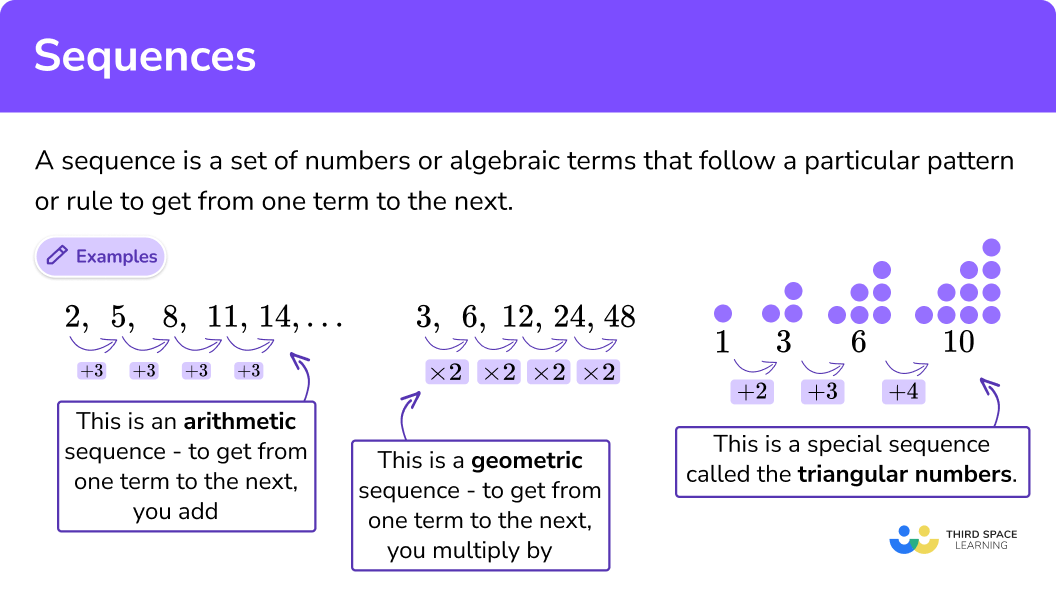
This is an arithmetic sequence since there is a common difference between each term. In this case, adding 5 to the previous term in the sequence gives the next term.
What is the formula for the sequence 4 9 14 19
The first term is 5×1 -1 = 4, : The second term is 5×2 -1 = 9 , : The third term is 5×3 – 1 and so on . So: The nth term is = 5n – 1.
Is 4 9 14 19 24 an example of a number sequence
arithmetic sequence
Answer and Explanation:
The given sequence is an arithmetic sequence. To properly check if it is indeed an arithmetic sequence, we have to take the difference between each term and each of their next terms.
What is the common difference of the sequence 4 9 14 19
5
Therefore, Common difference between 4 and 9 = |9-4| =5. Common difference between 9 and 14 = |14-9| =5. Common difference between 14 and 19 = |19-14| =5.
What is the nth term of 4 9 14 19 24 29
4,9,14,19,24,29,34,39,44, 49, 54, 59, 64, …
How would you describe the pattern 4 8 12 16 20 24
Infinite sequence: {4,8,12,16,20,24,…} The first term of the sequence is 4 . The "…" at the end indicates that the sequence goes on forever; it does not have a last term. It is an infinite sequence.
What is the pattern rule for 4 14 29 49
So, the rule can be described as adding a multiple of 5 to the previous term, starting with 10. 5. So, the next term in the sequence is 74. The sequence now looks like this: 4, 14, 29, 49, 74.
Which term of the sequence 4 9 14 19 is 124
25th term
Hence, 25th term of the given sequence is 124.
Which term of the following sequence 4 9 14 19 is 124
25th term
Hence, 25th term of the given sequence is 124.
Which term of the arithmetic progression 4 9 14 19 is 109
22nd term
Hence, 109 is the 22nd term of the Arithmetic Progression.
Which term of the sequence 4 9 14 19 is 299
Example 3: Which term of the A.P. 4, 9, 14, 19 … is 299 Solution: Here, first term (a) = 4 and common difference (d) = 5. Hence, 60th term of the given sequence is 299.
What is the math pattern for 1 4 9 16 25
All the numbers in the above pattern are square numbers i.e. they are numbers which are obtained when the number is multiplied with itself.The first term = 1 = 1×1.The second term = 4 = 2×2.The third term = 9 = 3×3.The fourth term = 16 = 4×4.So, the fifth term will be = 5×5 = 25.
What is the pattern of 4 8 12 16 20
This is an arithmetic sequence since there is a common difference between each term. In this case, adding 4 to the previous term in the sequence gives the next term. In other words, an=a1+d(n−1) a n = a 1 + d ( n – 1 ) . This is the formula of an arithmetic sequence.
What is the complete number pattern 1 4 9 16 25 49
Informally: When you multiply an integer (a “whole” number, positive, negative or zero) times itself, the resulting product is called a square number, or a perfect square or simply “a square.” So, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, and so on, are all square numbers.
What number would complete the pattern below 8 14 5 18 24 15 28 34
Summary: The number that would complete the pattern 14, 5, 18, 24, 15, 28, 34, __ is 25.
What are the next four terms in the sequence 1 4 9 16 _ _ _ _
1, 4, 9, 16, 25, 36, 49…
How many terms are there in the sequence 4 9 14 109
n=22. Hence, 109 is the 22nd term of the Arithmetic Progression.
What are the first 10 terms of the arithmetic sequence 4 9 14 19 24
4,9,14,19,24,29,34,39,44,49,54…
What is the sequence 1 4 5 9 14
Fifth term : 4+5=9, Sixth term : 5+9=14, Seventh term : 9+14=23, ∴ the missing term can be find by 14+23=37.
Which pattern does this sequence follow 1 4 9 16 25
So, the above sequence is a square number pattern.
What is the pattern rule for 1 4 9 16 25 36
Informally: When you multiply an integer (a “whole” number, positive, negative or zero) times itself, the resulting product is called a square number, or a perfect square or simply “a square.” So, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, and so on, are all square numbers.
What is the rule of 4 14 29 49
First, we need to identify the pattern or rule in the given sequence: 4, 14, 29, 49. 3. The differences between consecutive terms are increasing by 5 each time (10, 15, 20). So, the rule can be described as adding a multiple of 5 to the previous term, starting with 10.
What is the pattern of 4 9 16 25
Informally: When you multiply an integer (a “whole” number, positive, negative or zero) times itself, the resulting product is called a square number, or a perfect square or simply “a square.” So, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, and so on, are all square numbers.
What number would complete the pattern below 16 4 12 36 9 27 44 11
Given, the pattern 16, 4, 12, 36, 9, 27, 44, 11,……… We have to find the next number in the pattern. Let the next number be x. Therefore, the next number is 33.
What are the number patterns of 3 5 8 13 21
Fibonacci Numbers (Sequence):
1,1,2,3,5,8,13,21,34,55,89,144,233,377,… Fn=Fn−2+Fn−1 where n≥2 . Each term of the sequence , after the first two, is the sum of the two previous terms. This sequence of numbers was first created by Leonardo Fibonacci in 1202 .