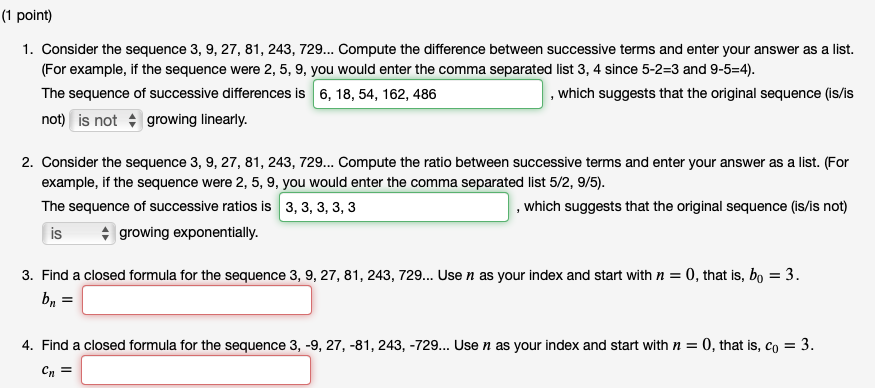
What kind of sequence is 3 9 27 81 243
This is a geometric sequence since there is a common ratio between each term. In this case, multiplying the previous term in the sequence by 3 gives the next term.
What is the sequence of 9 27 81
Given, the series 3, 9, 27, 81, 243,… is in geometric progression. We have to find the next number in the series. Here, the next number implies the 6th term of the series. Therefore, the next number in the series is 729.
What is the general term of the sequence 3 9 27 81
Summary: The next three terms of the sequence 3, 9, 27, 81, . . . are243, 729 and 2187.
Is the pattern 9 16 23 30 37 an arithmetic sequence
In this arithmetic sequence, the common difference d is 7. You can find this by subtracting a term from the consecutive term: 16 – 9 = 7, 23 – 16 = 7. In order to find the next four terms, keep adding 7 to the previous term. The next four terms are 30, 37, 44, and 51.
What is the nth term of the geometric sequence 9 27 81 243
This is a geometric sequence with a common ratio 3. That is you multiply by 3 each time to get the next term. the nth term is 3^n. 729.
What type of sequence is 3 11 19 27 35
This is an arithmetic sequence since there is a common difference between each term. In this case, adding 8 to the previous term in the sequence gives the next term.
What is the common ratio of the geometric sequence 3 9 27 81 81
Yes. It is a geometric sequence with initial term a0=3 and common ratio r=3 .
What is the complete sequence 9 18 27
9, 18, 27, 36, 45, , 63, 72.
What is 3 9 27 81 243 in sigma notation
The sigma notation of the expression 3-9+27-81+243 is given by 5(-1*3* 243 5(-1*3* 26-1)*+'3* 243 5(-1*+'3*
What is the sequence 9 16 24 33
So, it is true and the next number is 43. Note: For calculating the sequence of any continuous terms we always find the sequence rule first and then calculate the next values from that.
What is the rule for the arithmetic sequence 3 9 15 21 27
An arithmetic sequence is an ordered set of numbers that have a common difference between each consecutive term. For example in the arithmetic sequence 3, 9, 15, 21, 27, the common difference is 6. An arithmetic sequence can be known as an arithmetic progression.
What is the rule in finding the nth term in the sequence 1 3 9 27
The rule of the geometric sequence 1, 3, 9, 27, 81, 243, … is 3n where n is the n-th term in the sequence.
What is the next number in the sequence 9 16 24 33
So, it is true and the next number is 43. Note: For calculating the sequence of any continuous terms we always find the sequence rule first and then calculate the next values from that.
What kind of sequence is 6 11 18 27 38 51
Here's what we mean, consider the sequence: 6,11,18,27,38,51… looking at the first and "second differences" of this sequence would look like: Looking at this we can see that the second difference is constant, and not equal to zero, this means it is a quadratic sequence.
What type of sequence is 5 8 11 14 17
arithmetic sequences
Sequences of numbers that follow a pattern of adding a fixed number from one term to the next are called arithmetic sequences. The following sequences are arithmetic sequences: Sequence A: 5 , 8 , 11 , 14 , 17 , …
What is the common ratio of the sequence 243 81 27 9 3 1
This is a geometric sequence since there is a common ratio between each term. In this case, multiplying the previous term in the sequence by 13 gives the next term.
What is the pattern of 9 18 27 36 45
Arithmetic Number Patterns
This constant, or the difference between two consecutive numbers in an arithmetic number pattern, is a common difference. All multiplication tables are arithmetic number patterns. For instance, in the sequences 9, 18, 27, 36, 45, 54 … the common difference is 9.
What is the pattern rule of 9 18 27 36
This is an arithmetic sequence since there is a common difference between each term. In this case, adding 9 to the previous term in the sequence gives the next term.
What is sigma notation of geometric sequence
The reason why we want to start at n equals. 1 because if i plug in 1 in for n. That's 1 minus 1 is 0 negative 1 3 to the 0. Power is 1. 3 times 1 is going to give us 3 which gives our first. Term.
What type of math is sigma notation
Simple sum
The symbol Σ (sigma) is generally used to denote a sum of multiple terms. This symbol is generally accompanied by an index that varies to encompass all terms that must be considered in the sum. For example, the sum of first whole numbers can be represented in the following manner: 1 2 3 ⋯.
What kind of sequence is 9 18 27 36
This is an arithmetic sequence since there is a common difference between each term. In this case, adding 9 to the previous term in the sequence gives the next term.
What number sequence is 8 16 24 32
When we write the absolute values, the sequence would be eight, 16, 24, 32, and so on. This sequence of absolute values would be an arithmetic sequence. That's because there is a constant difference between any consecutive pair of terms.
What type of sequence is 3 9 15 21 27
arithmetic sequence
For example in the arithmetic sequence 3, 9, 15, 21, 27, the common difference is 6. An arithmetic sequence can be known as an arithmetic progression. The difference between consecutive terms is an arithmetic sequence is always the same.
What is the pattern of 9 15 21 27
This is an arithmetic sequence since there is a common difference between each term. In this case, adding 6 to the previous term in the sequence gives the next term.
What is the pattern rule of 1 3 9 27
The rule of the geometric sequence 1, 3, 9, 27, 81, 243, … is 3n where n is the n-th term in the sequence.