Jak Narysovat usu
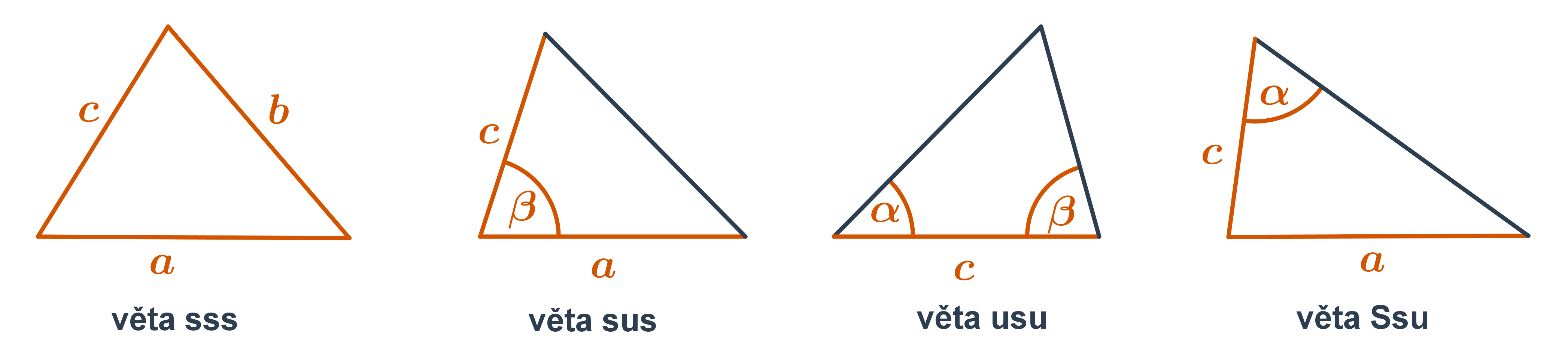
Věta usu: Shodují-li se dva trojúhelníky ve straně a v obou přilehlých úhlech, jsou shodné.
Archiv
Jak zní věta SSU
Věta Ssu: Shodují-li se dva trojúhelníky ve dvou stranách a úhlu proti větší z nich, jsou shodné.
Co je to věta SUS
Pokud se dva trojúhelníky shodují ve dvou stranách a úhlu, který strany svírají, jsou shodné (věta sus).
Jak se počítá věta SUS
Pro každý trojúhelník ABC s vnitřními úhly α, β, γ a stranami a, b, c platí: a / sin(α) = b / sin(β) = c / sin(γ). Důkaz je pro přehlednost uveden zvlášť. Sinová věta je jednoduchá, elegantní a navíc i velmi užitečná.
Jak se počítá podobnost
Dva geometrické útvary nazýváme podobné, jestliže poměry délek všech dvojic odpovídajících si úseček těchto útvarů se rovnají témuž číslu k > 0. Toto číslo nazýváme poměr podobnosti. Každé dva odpovídající si úhly podobných útvarů jsou shodné.
Jak se značí podobnost
Jestliže jsou poměry všech sobě odpovídajících stran trojúhelníků shodné, pak jsou tyto trojúhelníky podobné. Konstanta k je poměr podobnosti. ΔABC ~ ΔA´B´C´ Čteme: trojúhelník ABC je podobný trojúhelníku A´B´C´.
Co je SSU
Informace o zkratce 'SSÚ'
Správní úřad s působností ve věcech pozemních komunikací.
Co je to podobnost
Podobnost lze popsat i matematicky. Dva geometrické útvary nazýváme podobné, jestliže poměry délek všech dvojic odpovídajících si úseček těchto útvarů se rovnají témuž číslu k > 0. Toto číslo nazýváme poměr podobnosti. Každé dva odpovídající si úhly podobných útvarů jsou shodné.
Kdy jsou trojúhelníky podobne
Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné.
Co je to věta SSS
Věta sss: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné.
Jak poznat podobnost
Podobnost lze popsat i matematicky. Dva geometrické útvary nazýváme podobné, jestliže poměry délek všech dvojic odpovídajících si úseček těchto útvarů se rovnají témuž číslu k > 0. Toto číslo nazýváme poměr podobnosti. Každé dva odpovídající si úhly podobných útvarů jsou shodné.
Jak se určuje poměr podobnosti
Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné. Je-li poměr podobnosti k ˃ 1, jedná se o zvětšení. Je-li poměr podobnosti k ˂ 1, jedná se o zmenšení.
Jak sestrojit trojúhelník SSU
Věty o sestrojitelnosti trojúhelníků: ➢ Věta SSS: Trojúhelník lze sestrojit podle věty SSS, jsou-li dány 3 jeho strany, pro které platí trojúhelníková nerovnost. ➢ Věta SUS: Trojúhelník lze sestrojit podle věty SUS, jsou-li dány 2 jeho strany a úhel jimi sevřený. Velikost zadaného úhlu je menší než 180°.
Jak určit poměr podobnosti
Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné. Je-li poměr podobnosti k ˃ 1, jedná se o zvětšení.
Jak zapsat podobnost
Jestliže jsou poměry všech sobě odpovídajících stran trojúhelníků shodné, pak jsou tyto trojúhelníky podobné. Konstanta k je poměr podobnosti. ΔABC ~ ΔA´B´C´ Čteme: trojúhelník ABC je podobný trojúhelníku A´B´C´. Příklad: Je dán ΔABC: a = 28,2cm; b = 25,3 cm; c = 48,4 cm.
Co znamená kdyz jsou trojúhelníky podobne
VĚTA sus Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících si stran a shodují se v úhlu jimi sevřeném, jsou podobné.
Jak sestrojit trojúhelník SSS
Věty o sestrojitelnosti trojúhelníků: ➢ Věta SSS: Trojúhelník lze sestrojit podle věty SSS, jsou-li dány 3 jeho strany, pro které platí trojúhelníková nerovnost. ➢ Věta SUS: Trojúhelník lze sestrojit podle věty SUS, jsou-li dány 2 jeho strany a úhel jimi sevřený. Velikost zadaného úhlu je menší než 180°.
Kdy jsou dva trojúhelníky shodne
Věta sss: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné. Věta usu: Dva trojúhelníky, které se shodují v jedné straně a úhlech přilehlých k této straně, jsou shodné.
Jak se pocita poměr podobnosti
Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné. Je-li poměr podobnosti k ˃ 1, jedná se o zvětšení. Je-li poměr podobnosti k ˂ 1, jedná se o zmenšení.
Co je to shodnost trojúhelníků
Shodují-li se dva trojúhelníky ve dvou stranách a úhlu proti delší z nich, jsou shodné.
Jak se zapisuje podobnost
Jestliže jsou poměry všech sobě odpovídajících stran trojúhelníků shodné, pak jsou tyto trojúhelníky podobné. Konstanta k je poměr podobnosti. ΔABC ~ ΔA´B´C´ Čteme: trojúhelník ABC je podobný trojúhelníku A´B´C´. Příklad: Je dán ΔABC: a = 28,2cm; b = 25,3 cm; c = 48,4 cm.
Kdy jsou trojúhelníky podobně
Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné.
Jak popisujeme trojúhelník
Trojúhelník je geometrický útvar, skládající se ze tří vrcholů a tří stran. Pokud leží trojúhelník v Euklidovském prostoru v rovině, je součet velikostí jeho vnitřních úhlů roven 180° (1 π) a libovolné tři body Euklidovské roviny, které neleží na přímce, jsou vrcholy právě jednoho trojúhelníka.
Co to je koeficient podobnosti
Poměr vzdálenosti dvou bodů daného geometrického útvaru a vzdálenosti odpovídajících dvou bodů jiného geometrického útvaru (referenčního) je u podobných útvarů shodný pro každou takovou dvojici bodů a nazývá se koeficient podobnosti.
Co jsou to shodné útvary
Jestliže dva rovinné útvary můžeme přemístit tak, že se kryjí,budeme je nazývat shodnými útvary. Jestliže se dva trojúhelníky shodují ve všech třech stranách, pak jsou shodné. Jestliže se dva trojúhelníky shodují ve dvou stranách a úhlu jimi sevřeném, pak jsou shodné.