Merkle medis leidžia kompiuterių tinkle patikrinti atskirus įrašus, neperžiūrint ir nelyginant visos duomenų bazės versijų. Jie tai daro naudodami kriptografiją, kuri atskleidžia atskirą įrašą, kartu garantuodama, kad visi kiti duomenų bazės įrašai nebuvo pakeisti. Pirmą kartą Ralphas Merkle užpatentuotas 1979 m., Merkle medžiai buvo svarbus raktas į duomenų bazės patikrinimą per visą kompiuterių istoriją.
„Merkle Trees“ yra ypač naudinga paskirstytuose tinkluose, kur keli kompiuteriai saugo tos pačios duomenų bazės ar knygos kopijas. Kai Satoshi sukūrė „Bitcoin“, „Merkle“ medžio naudojimas sandorio tikrinimui buvo nereikalingas. Dėl paskirstyto blokų grandinės pobūdžio mums reikia saugaus ir greito būdo įsitikinti, kad visi tinklo nariai turi tą pačią knygą.
Jei studijavote „blockchain“, tikriausiai girdėjote apie Merklės medžius ir Merklės šaknis. Tačiau daugelis investuotojų ir entuziastų nežino, kaip jie veikia. Atsižvelgiant į tai, kad jie yra pagrindinė „blockchain“ saugumo ir pasitikėjimo dalis, verta suprasti pagrindus. Šis išradingas mechanizmas leidžia saugoti ir gauti milijonus „blockchain“ operacijų.
Efektyvaus patikrinimo poreikis
Pradėkime nuo pagrindų. Kodėl mums reikia Merkle medžių ir kuo jie naudingi „blockchain“ kontekste?
Norėdami atsakyti į šį klausimą, apsvarstykite pasaulį, kuriame nebūtų Merkle medžių. Jei „Bitcoin“ neturėjo „Merkle“ medžių, kiekvienas tinklo mazgas turėtų išsaugoti išsamią visų operacijų, kurios kada nors įvyko su „Bitcoin“, kopijas. Tuomet, patvirtindamas ankstesnę operaciją, mazgas turėtų kreiptis į tinklą ir iš savo bendraamžių gauti knygos knygą. Norėdamas įsitikinti, kad tinklo knygos tiksliai atitinka, mazgas turėtų kiekvieną eilutę palyginti su savo įrašais. Jei praslystų kokie nors pakeitimai, tai pakenktų tinklo saugumui.
Kadangi norint patvirtinti duomenis reikia turėti pačius duomenis, kiekvienai „Bitcoin“ patvirtinimo užklausai reikės, kad per tinklą būtų išsiųsti milžiniški informacijos paketai. Tada patvirtinančiam kompiuteriui reikės skirti apdorojimo galią knygų palyginimui, kad įsitikintumėte, jog nėra pakeitimų.
Merklės medžiai išsprendžia šią problemą sukaupdami įrašus knygoje. Tai veiksmingai atsieja duomenų įrodymą nuo pačių duomenų. Šie maišos yra dydžiais mažesni už pačią knygą, todėl įrodant operacijos galiojimą reikia siųsti mažus paketus tik per tinklą. Tai leidžia įrodyti, kad dvi knygos knygos versijos atitinka minimalią skaičiavimo galią ir tinklo pralaidumą.
Jei tai skamba puikiai, tai yra taip. Merkle medžiai yra tikrai šaunus kriptografinis išradimas. Taigi dabar kyla klausimas, kaip jie veikia?
Greitas atnaujinimas apie maišymą
Prieš įsigilinant į Merkle medžių detales, maišant reikia kriptografinių pamatų. „Blockchains“ naudoja maišymą visur, pradedant darbo algoritmų įrodymu ir baigiant failų patikrinimu. Maišymas yra kertinis šiuolaikinės kriptografijos akmuo.
Per daug nepatekęs į piktžoles maiša yra tam tikro tipo algoritmas, reikalaujantis bet kokio įvesties, neatsižvelgiant į ilgį, ir išvestas standartinio ilgio atsitiktine išvestimi. Pavyzdžiui, „Bitcoin“ operacija „Alisa siunčia Bobui 1 BTC“ atrodo kaip atsitiktinių simbolių eilutė:
„3cbcf3e1075b0b3357140de438336733bd6927cd1e78d36cc278324fcce932ad“
Ši simbolių eilutė yra maišos ir tai lemia. Tai reiškia, kad „A -> B 1BTC “visada maišo tą pačią išvestį.
Tačiau maišos turi dar vieną puikią savybę. Net nedidelis įvesties pokytis lavina į drastišką išėjimo pokytį. Jei šiek tiek pakeisime operaciją į „A-> B 1.1BTC “, tada maiša tampa visiškai kitokia. Todėl iškart akivaizdu, ar įrašą pakeitė net vienas veikėjas.
Maišos yra nuostabios ir dėl kitų priežasčių, tačiau norint suprasti, kaip veikia Merkle medis, pakanka suprasti, kad maišos yra deterministinės, o pokyčiai sukelia krioklį..
Kaip jūs padarote Merkle medį
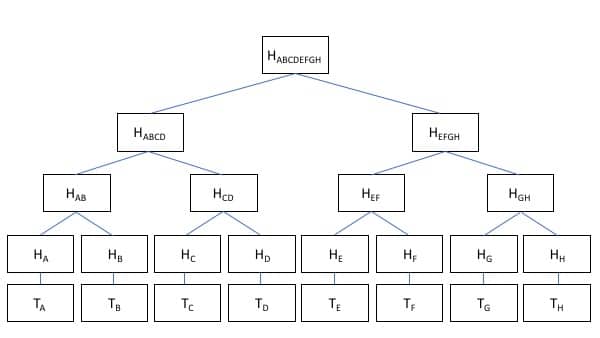
Merkle medis. „Blockchain Merkle“ medžiuose yra tūkstančiai maišų. Čia pavaizduotos tik 8 nuotraukos.
Dabar atėjo laikas pastatyti mūsų Merkle medį. Allice / Bob operaciją pavadinsime aukščiau „Operacija A.“ Kai ta operacija įtraukiama į blokų grandinę, ji tampa bloko dalimi su kitomis operacijomis. Paprastumo dėlei šias operacijas vadinsime tiesiog B, C ir D.
Kiekviena iš šių operacijų maišoma, todėl neturime laikytis išsamios informacijos, kas ir kiek buvo sandoris. Bet mes vis tiek galime įrodyti, kad sandoris nebuvo sugadintas, nes mes turime visas maišas. Dabar mes turime H (A), H (B), H (C) ir H (D).
Laikymasis ant keturių maišų nėra toks didelis dalykas. Tačiau kiekviename „Bitcoin“ bloke yra apie 2 000 operacijų, todėl visų tų maišų laikymasis ir perdavimas yra per didelis saugojimas ir pralaidumas. Merkle medis išsprendžia šią problemą suporuodamas sandorius ir sujungdamas juos.
Dabar H (A) + H (B) = H (AB) ir H (C) + H (D) = H (CD). Derindami ir kaupdami sandorius, perpus sumažinome maišų, kurias turime saugoti, skaičių. Mes galime padaryti tą patį dar kartą, taigi H (AB) + H (CD) = H (ABCD). Taip elgdamiesi dabar turime tik vieną maišos įrašą, kuris yra deterministinis, remiantis visų pagrindinių operacijų maiša. Šis vienintelis maišas vadinamas Merkle šaknimi.
Operacijų patikrinimas naudojant Merkle šaknį
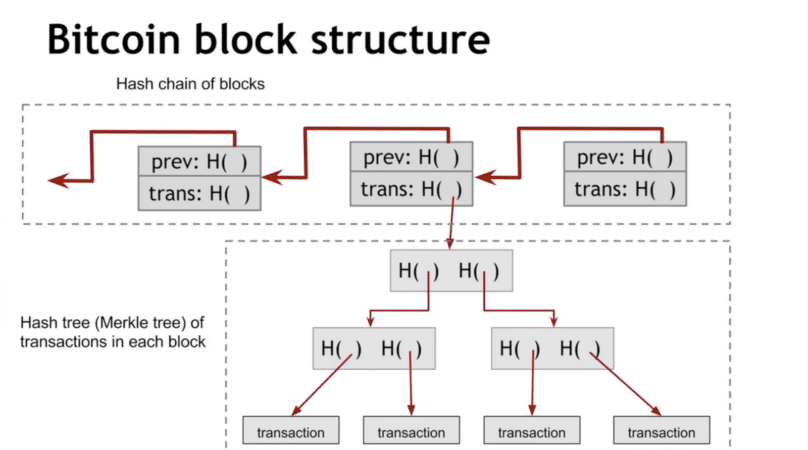
„Merkle“ medžio šaknies maišos yra pagrindinė kiekvieno „Bitcoin“ bloko dalis, susieta su kitu grandinės bloku.
Kiekviename „Bitcoin“ bloke yra „Merkle“ šaknis, esanti bloko antraštėje. Tai kaip mes patikriname bloko turinį ir kelių knygų nuoseklumą. Jei mano „blockchain“ egzemplioriuje yra ta pati „Merkle“ šaknis blokui, kaip ir jūsų bloko grandinės kopijoje, mes žinome, kad visos to bloko operacijos yra vienodos, ir mes sutariame dėl knygos. Net nedidelis nenuoseklumas sukeltų labai skirtingas Merkle šaknis dėl maišos savybių.
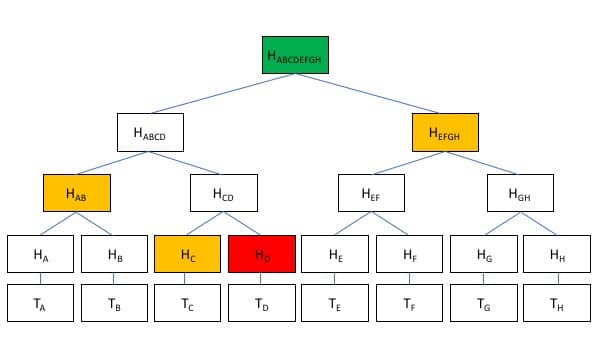
Norint patvirtinti D operaciją, reikia žinoti tik H (AB), H (C), H (D) ir H (EFGH).
Jei yra Merkle šaknies neatitikimas, galiu paprašyti patikimos institucijos dviejų sub-maišų. Iš to galime susiaurinti įrašą, dėl kurio nesutinkame, paprašydami papildomų maišų. Dėl to mes galime nustatyti neatitikimus, nereikėdami eiti eilutė po eilutės per visą knygą.
Išvada
Blokų grandinės, duomenų bazės ir tinklai visame pasaulyje naudoja Merkle medžius, kad greitai ir efektyviai koordinuotų įrašus keliuose kompiuteriuose. Dabar, kai suprantate pagrindus, lengva suprasti, kodėl toks duomenų struktūrizavimo būdas daro blokų grandinę saugią ir efektyvią.